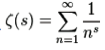„Ich weiß, dass ich nichts weiß!“ Doch was genau wissen wir nicht? Wir fragen Heidelberger Wissenschaftler nach den großen, ungelösten Problemen der Wissenschaft. Teil I der neuen Serie.
[box type=“shadow“ ]

Bei Intelligenztestleistungen ist bekannt, dass sich diese von Generation zu Generation in den westlichen Industrieländern verbessern. Im Schnitt werden die Ergebnisse eines Tests alle zehn Jahre um etwa fünf Punkte besser. Dieses Phänomen, genannt Flynneffekt, wird seit den Zwanziger Jahren beobachtet und setzt sich in allen beobachteten Ländern mit Ausnahme Skandinaviens fort. Dieser Effekt ist aus mehreren Gründen rätselhaft. Wenn Sie beispielsweise rückwärts rechnen und wir heute einen Durchschnitts-IQ von 100 annehmen, so würde das bedeuten, vor 100 Jahren hätten die Menschen einen Durchschnitts-IQ von 50 gehabt. Damit hätte niemand die Schule oder ein Studium abschließen können. Eine praktische Konsequenz ist, dass wir unsere Intelligenztests alle zehn Jahre kostspielig neu normieren müssen. Denn sonst würden wir immer höhere und höhere Ergebnisse als Testwerte bekommen, man müsste fast sagen, unabhängig vom tatsächlichen Leistungsvermögen. Auch die Ursachen dieses Effekts sind rätselhaft. Als Erklärung werden gerne Umweltfaktoren im Sinne einer verbesserten Lernumgebung herangezogen. Im Widerspruch dazu steht, dass der Anstieg sich vor allem in der fluiden Intelligenz zeigt. Als fluide Intelligenz bezeichnet man nach dem Psychologen Raymond Cattell die Grundausstattung an Intelligenz, die nicht durch Bildung und Lernerfahrung verändert wird. Genauso wenig kann die verbesserte Ernährungssituation den Flynneffekt erklären. Denn der Effekt tritt in afrikanischen Ländern auf, in denen sich die Ernährungssituation nicht verändert hat. Außerdem hielt er in Europa vor, während und nach dem ersten Weltkrieg an, als die Ernährungssituation katastrophal war. Auch genetische Faktoren ändern sich nicht schnell genug, um pro Generation einen so großen Zuwachs zu verursachen. Keine Erklärung ist demnach konsistent mit den empirischen Daten.[/box]
[box type=“shadow“ ]

Die Entschlüsselung der DNA-Sequenz (des sogenannten genetischen Codes) des menschlichen Genoms zeigte, dass der Mensch „nur“ ca. 20.000 bis 25.000 Gene besitzt, die in ca. 10 bis 15 Prozent der DNA-Sequenz stecken. Diese Gene sind bei allen Menschen normalerweise gleich. Eines der großen Rätsel der Wissenschaft ist daher die Frage nach der Bedeutung der restlichen 85 bis 90 Prozent. Lange Zeit hielt man dies für Müll der Evolution, da diese nicht-genkodierenden Sequenzen mit der Komplexität des Lebens zugenommen haben, womit wir bei Fragen der Lebensentwicklung in der Astrobiologie wären. Wo ist jedoch die Individualität im Genom versteckt, d.h. wo steht, dass wir unseren Eltern oder Großeltern ähnlich sehen? Und warum wird dieser „Müll“ von der Zelle so intensiv gepflegt und erhalten? Mehr noch, es gibt Krankheiten, die dadurch entstehen, dass sich wenige Sequenzen in diesem Teil des Genoms verändern. Man vermutet, dass dies die räumliche Struktur im Genom so verändert, dass das Funktionieren von Genen beeinflusst wird. So scheint – und damit kommen wir zur Biophysik – diese „dunkle“ Materie des Lebens entscheidend die 3D-Struktur und Organisation von Genomen zu bestimmen. Es scheint also in der DNA-Sequenz die Information der 3D-Architektur zu stecken, die das Leben neben epigenetischen Mechanismen zur Kodierung von Information und Funktionen nutzt. Mit einer Vielzahl moderener Techniken und theoretischen Modellen versucht die Biophysik die Architektur des Genoms und die Geheimnisse der nicht-kodierenden Sequenzen zu erfoschen.[/box]
[box type=“shadow“ ]

Ein großes Rätsel in den Neurowissenschaften ist der „Code“, in dem Nervenzellen miteinander kommunizieren und Informationen speichern. Wir wissen auf zellulärer Ebene gut, wie Nervenzellen funktionieren und miteinander verschaltet sind. Wir wissen auch, dass Verknüpfungen zwischen gleichzeitig aktiven Nervenzellen verstärkt werden und dass dies die neuronale Basis des Lernens darstellt. Allerdings haben wir bis heute keine Möglichkeit, aus der Aktivität von Nervenzellen oder Gehirnarealen abzulesen, woran genau eine Person gerade denkt oder woran sie sich erinnert. Wenn wir wüssten, wo welche Informationen im Gehirn gespeichert sind, könnten wir potenziell gezielt Inhalte abrufen, die Erinnerungsleistung unterstützen oder traumatische Erfahrungen löschen. Natürlich würde das wiederum ethische Fragen aufwerfen.[/box]
[box type=“shadow“ ]

Das Gehirn ist ein Universum aus etwa 100 Milliarden Zellen und zehntausend mal mehr synaptischen Verbindungen. Es verarbeitet Information mit einer Leistungsaufnahme von nur 30 Watt und benötigt dazu keine vorgefertigten Algorithmen, sondern organisiert sich selbst durch stetige Wechselwirkung mit der Umgebung. Ein fundamentales Verständnis der Informationsverarbeitung im Gehirn und eine Übertragung ihrer Prinzipien auf synthetische Systeme gehört zweifelsohne zu den zentralen wissenschaftlichen Herausforderungen des 21. Jahrhunderts. Ähnlich wie beim richtigen Universum erfordert ein experimenteller Zugang technisch aufwendige Methoden wie abbildende Verfahren oder Computersimulationen. Unsere Heidelberger Gruppe verfolgt einen neuen Weg, indem sie physikalische Modelle neuronaler Schaltkreise als mikroelektronische Systeme realisiert. Solche so genannten neuromorphen Systeme sind fundamental verschieden von traditionellen Computern, die nach dem Prinzip der Turing-Maschine funktionieren. Wie das biologische Vorbild weisen sie hohe Energieeffizienz, die Fähigkeit zur Selbstorganisation und Fehlertoleranz auf. Besonders spannend ist die Möglichkeit, den Lauf der Zeit verglichen zu unserer biologischen Echtzeit um einen Faktor von 1000 bis 10000 zu komprimieren. Lernprozesse, die in der Natur Tage dauern und auf Supercomputern praktisch nicht simuliert werden können, finden auf neuromorphen Computern in Sekunden statt. Ziel der Forschung ist ein fundamentales Verständnis der Informationsverarbeitung im Gehirn sowie der Bau von neuartigen Computern.[/box]
[box type=“shadow“ ]

Die Riemann’sche Vermutung: In Analogie zu den 23 Jahrhunderproblemen, die David Hilbert im Jahr 1900 vorstellte, lobte im Jahr 2000 das Clay Mathematics Institute für die Lösung von je einem von sieben so Milleniumsproblemen ein Preisgeld von einer Million US-Dollar aus. Das einzige Problem, das in beiden Listen auftaucht, ist die zuerst 1859 von Bernhard Riemann formulierte Riemann’sche Vermutung, die eine Aussage über die Nullstellenverteilung der Riemann’schen Zetafunktion macht. Letztere ist auf der rechten Halbebene der komplexen Zahlen mit Realteil größer 1 definiert durch die unendliche Reihe
und lässt sich mit Ausnahme einer Polstelle bei s = 1 analytisch auf ganz C fortsetzen. Hierbei lassen sich die Funktionswerte für Realteil kleiner 0 über eine Funktionalgleichung aus denen für Realteil größer 1 bestimmen, so dass das Verhalten der Zetafunktion außerhalb des kritischen Streifens 0 ≤ Re(s) ≤ 1 gut bekannt ist. Die Riemann’sche Vermutung besagt nun, dass alle Nullstellen innerhalb des kritischen Streifens Realteil 1 haben. Ein Beweis der Riemann’schen Vermutung hätte enorme Auswirkungen auf die Mathematik, und hier zuvorderst auf die Zahlentheorie, in der unzählige Arbeiten ihre Richtigkeit voraussetzen. Recht direkt folgt aus der Riemann’sche Vermutung etwa die bestmögliche Fehlerabschätzung für den Primzahlsatz, so dass sich die Anzahl der Primzahlen mit einer festgelegten Anzahl von Stellen besser abschätzen lässt. Dies wiederum ermöglicht eine bessere Abschätzung für die Sicherheit von Verschlüsselungsalgorithmen, die als Schlüssel Primzahlen einer gegebenen Größe benutzen. Die große Mehrheit der MathematikerInnen glaubt heute an die Richtigkeit der Riemann’schen Vermutung, für die es mittlerweile auch überzeugende Indizien gibt. So weiß man seit dem Jahr 2004, dass die ersten zehn Billionen Nullstellen (von der reellen Achse aus gerechnet) allesamt Realteil 1 aufweisen. Wie ein erfolgreicher Beweis ansetzen muss, ist jedoch immer noch unklar: Es ist etwa bis heute nicht gelungen, die Existenz eines 0 < ε < 1 zu zeigen, für dass alle Nullstellen innerhalb des kritischen Streifens ε < Re(s) < 1 − ε erfüllen.[/box]
zusammengestellt von Janina Schuhmacher